конспекты занятий по курсу

 «Теория и реализация языков программирования»

Занятие 5

^

=

_

5. Регулярные языки (продолжение)

5.1. Всюду определённые (полные) ДКА

На вход алгоритма минимизации ДКА требуется всюду определённый или, как его ещё называют, полный ДКА.

Под полным ДКА подразумевается ДКА, у которого

d (A, a) ≠ Æ   "   A Î Q и    "   a Î T.

Доказано ([1]), что полный ДКА всегда может быть получен из неполного следующим образом:

а. Добавляем к неполному ДКА новое незавершающее состояние Z.

б. Функции перехода полного ДКА получаем следующим образом

1) "   A Î Q и    "   a Î T, которым соответствует  d (A, a) ≠ Æ  

сохраняем старую функцию переходов: d¢ (A, a) = d (A, a).  

2)  "   A Î Q и    "   a Î T, которым соответствует  d (A, a) = Æ

добавляем функцию перехода в новое состояние: d¢ (A, a) = Z.

3) "   a Î T добавляем функцию перехода из нового состояния Z в него же:

d¢ (Z, a) = Z   (" a Î T).

5.2. Алгоритм минимизации полного ДКА

Алгоритм минимизации полного ДКА состоит в следующем [1]:

(1) Построить начальное разбиение множества состояний из двух групп:

заключительные состояния {F} и остальные {Q-F}.

(2) Для каждой имеющейся группы G разбить G на подгруппы так, чтобы состояния s  и t из G оказались в одной подгруппе тогда и только тогда, когда для каждого входного символа a состояния s и t имеют переходы по a в состояния из одной и той же ранее найденной нами группы;

заменить G на множество всех полученных подгрупп;

(3) Если при выполнении (2) не удалось разбить ни одной группы, переходим к шагу 4,

иначе повторяем шаг 2.

(4) Определим новые состояния ДКА, как получившиеся группы состояний минимизируемого автомата.

Если группа содержит начальное состояние автомата M, то эта группа становится начальным состоянием автомата M'. Если группа содержит заключительное состояние M, она становится заключительным состоянием M'.

Отметим, что каждая полученная группа либо состоит только из состояний из {F}, либо не имеет состояний из {F}. Переходы определяются очевидным образом.

(5) Если M' имеет «мёртвое» состояние, то есть  состояние, которое не является допускающим и из которого нет путей в допускающие, удалить его и связанные с ним переходы из M'.

Удалить из M' также все состояния, недостижимые из начального.

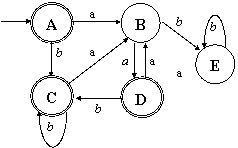
Пример 5.1. Минимизация ДКА для языка {x Î {a, b}* : |x|_a – чётно}

Как мы успели заметить, ДКА, полученный по алгоритму из НКА, соответствующий РВ (ab*a | b)*, явно имеет избыточные состояния.

Поскольку этот ДКА оказался полным, к нему можно применить алгоритм минимизации полного ДКА:

 (1) Построим начальное разбиение множества состояний из двух групп:

заключительные состояния F =  {A, C, D}

и остальные Q-F = {B, E}.

Рис. 5.1. ДКА, полученный по алгоритму из НКА, соответствующий РВ (ab*a | b)*

 (2-3). Выполнение шагов (2) и (3) алгоритма удобно отслеживать на диаграмме, по горизонтальной оси которой выписывается перечень всех вершин ДКА от первой до предпоследней, а по вертикальной (сверху вниз) – от второй до последней.

B

×

C

0

×

D

0

×

0

E

×

0

×

×

A

B

C

D

Рис. 5.2. Диаграмма определения равнозначных (эквивалентных) состояний для минимизируемого ДКА.

Знаком × здесь обозначены неравнозначность состояний, знаком 0 – равнозначность.

Первый раз они проставляются так.

Пусть у нас обе группы состояний не пусты, т.е. F ≠ Æ и Q-F ≠ Æ (иначе имеем вырожденные случаи, соответственно, с ничего не принимающим ДКА и, во втором случае, с ДКА, все состояния которого равнозначны, т.е. ДКА с единственным состоянием, которое является и входным и заключительным).

Тогда на пересечении каждого состояния из F с каждым состоянием из Q - F ставим × (поскольку они уже принадлежат к разным группам состояний).

В нашем примере

F =  {A, C, D}, а 

Q–F = {B, E},

поэтому, скажем, состояния А и В, А и Е изначально являются неэквивалентными:

B

×

C

×

D

×

E

×

×

×

A

B

C

D

После этого к наметившимся кандидатам в равнозначные состояния (C и A, D и A, D и C, E и B) применяем шаг 2 Алгоритма минизации до тех пор, пока удаётся получать новые разбиения состояний.

Например, для пары С и А, проверяем – нет ли переходов из них по знаку «a» в разные группы состояний.

d (A, a) = B

d (C, a) = B

По знаку «a» попадаем не только в одну группу состояний, но даже в одно и тоже состояние, разницы нет.

Проверяем переходы по знаку «b»:

d (A, b) = C

d (C, b) = C

Также нет разницы.

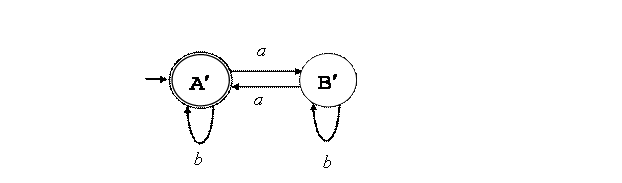
Тот же итог для данного примера имеем и для других пар. Разбиение закончено.

(4) Определим новые состояния ДКА, как получившиеся группы состояний минимизируемого автомата.

A¢ =  {A, C, D} 

B¢ = {B, E}

Минимизированный автомат будет иметь вид

Рис. 5.3. Минимизированный ДКА.

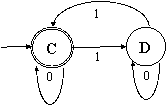
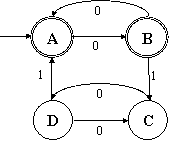
Задача 5.1. Исследуйте возможность минимизации следующего ДКА:

 5.3. Примеры задач на регулярные языки

Пример 5.2. Построить ДКА для языка {x Î {0, 1}* : на каждом кратном двум месте цепочки которого (1, 3, 5, …) стоит знак 0 (нумерация знаков начинается с 1), а |x|₁ – чётно}.

Самые короткие цепочки из данного языка такие:

e, 0, 00, 000, 0000, 0101 и т.д.

Не будем торопиться переходить к решению этой, в общем-то, простой задачи, а сначала постараемся разобрать её условие, понять, что оно может нам подсказать о будущих свойствах ДКА или ПГ, которые соответствуют данному языку.

Заметим, что в условии задачи указаны два ограничения, одно из которых касается нулей, второе – единиц.

По нулям имеем следующие состояния:

А – мы на кратном двум месте цепочки (начиная с 1-го), здесь должен стоять 0

B – мы на некратном двум месте, здесь может стоять как 0, так и 1.

Рис. 5.4. ДКА для подмножества искомого языка {x Î {0, 1}* : на каждом кратном двум месте цепочки которого (1, 3, 5, …) стоит знак 0 (нумерация знаков начинается с 1).

По единицам состояния таковы:

С – в данное время принято (порождено)  чётное число единиц, это состояние может быть завершающим.

D - |x|₁ – нечётно, состояние не может быть завершающим.

Рис. 5.5. ДКА для подмножества искомого языка {x Î {0, 1}* : |x|₁ – чётно).

Учёт каждого из этих ограничений по отдельности требует самое меньшее двух состояний. Поскольку ни одно из ограничений не зависит от другого, то комбинаторика подсказывает, что искомый ДКА должен содержать хотя бы    2 × 2 = 4   состояния.

Попробуем их перечислить:

А - кратное двум место цепочки, |x|₁ – чётно. Состояние завершающее.

B - некратное двум место цепочки, |x|₁ – чётно. Состояние завершающее

С - кратное двум место цепочки, |x|₁ – нечётно. Состояние не завершающее

D - некратное двум место цепочки, |x|₁ – нечётно. Состояние не завершающее

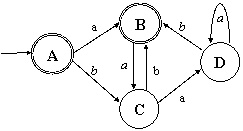
Рис. 5.6. ДКА – итог перемножения двух частных ДКА - подмножеств искомого языка.

Задача 5.2. Построить ДКА для языка {x Î {0, 1}* : на каждом кратном трём месте цепочки которого (1, 4, 7, …) стоит знак 0 (нумерация знаков начинается с 1), а |x|₁ – чётно}. Исследовать полученный ДКА на минимальность состояний.

Совет. Познакомьтесь с более кратким математическим описанием соответствующих алгоритмов в пособии [1] и введёнными при этом понятиями и обозначениями.

== Ссылки ==

[1] Серебряков В.А. [и др.]. Теория и реализация языков программирования. М.: МЗ-Пресс, 2003 (1-е изд.) и 2006 (2-е изд). – 294 c. (681.3/ Т33).

^

=

_