|
|
конспекты занятий
по курсу «Теория и
реализация языков программирования» Занятие 3 |
|
|||
|
|
|
||||
|
|
3. Регулярные языки и их описание Познакомившись
вкратце с различными видами формальных грамматик и языков, перейдём к более
подробному их изучению, начиная с самых простых языков и способов их задания.
Регулярные
языки
могут быть заданы: ·
регулярными множествами и выражениями; ·
конечными автоматами; ·
праволинейными и леволинейными грамматиками. 3.1. Регулярные
множества и выражения Определение. Регулярное множество в алфавите T
определяется рекурсивно так: (1) {Æ} (пустое
множество) – регулярное множество (РМ) в алфавите T; (2) {e} – РМ в алфавите
T (e – пустая
цепочка); (3) {a} – РМ в алфавите T для каждого a Î T; (4) если P и Q – РМ в алфавите T, то регулярными являются
и множества (а) P È Q (объединение (union, sum)), (б) PQ (сцепление (concatenation), то есть множество { pq | pÎ
P, qÎQ}), (в) P* (повторение (iteration): (5) ничто другое не является регулярным множеством в
алфавите T. Итак, множество в алфавите T регулярно тогда и только тогда, когда оно либо Æ, либо e, либо {a} для некоторого a Î T, либо его можно получить из этих
множеств применением конечного числа операций объединения, конкатенации и
итерации. Приведённое выше определение регулярного множества
позволяет ввести следующую удобную форму его записи, называемую регулярным
выражением. (1) Æ – регулярное
выражение (РВ), обозначающее регулярное множество (РМ) {Æ}; (2) e – РВ,
обозначающее РМ {e}; (3) a – РВ,
обозначающее РМ {a}; (4) если p и q – РВ, обозначающие регулярные
множества P и Q соответственно, то: (а) (p | q) – РВ, обозначающее регулярное множество PÈQ, (б) (pq) – РВ, обозначающее РМ PQ, (в) (p*) – РВ, обозначающее РМ P*; (5) ничто другое не является регулярным выражением в
алфавите T. В регулярных выражениях опускают лишние скобки с учётом
того, что наивысшее предпочтение (priority) имеет операция
итерации, затем идёт конкатенация, и лишь затем - объединение. Мы также будем пользоваться сокращением p+ для обозначения pp* (т.е. все итерации кроме пустой
цепочки). Примеры. Несколько примеров регулярных выражений и обозначаемых ими
регулярных множеств: а) a(e|a)|b –
обозначает множество {a, b, aa}; б) a(a|b)* – обозначает множество всевозможных цепочек,
состоящих из a
и b,
начинающихся с a; в) (a|b)*(a|b)(a|b)* – обозначает множество всех непустых
цепочек, состоящих из a и b, то есть множество {a, b}+; г) ((0|1)(0|1)(0|1))* – обозначает множество всех цепочек,
состоящих из нулей и единиц, длины которых делятся на 3. Ясно, что для каждого регулярного множества можно найти
регулярное выражение, обозначающее это множество, и наоборот. Более того, для
каждого регулярного множества существует бесконечно много обозначающих его
регулярных выражений. Будем говорить, что регулярные выражения равны или
эквивалентны (=), если они обозначают одно и то же регулярное множество. Существуют алгебраические законы, позволяющие осуществлять
эквивалентное преобразование регулярных выражений. Пусть p, q и r – регулярные выражения. Тогда справедливы
следующие соотношения: |
|
|||
|
|
(1) p|q = q|p; (2) Æ* = e; (3) p|(q|r) = (p|q)|r; (4) p(qr) = (pq)r; (5) p(q|r) = pq|pr; (6) (p|q)r = pr|qr; |
(7) pe = ep = p; (8) Æ p = pÆ = Æ; (9) p* = p|p*; (10) (p*)* = p*; (11) p|p = p; (12) p| Æ = p. |
|
||
|
|
Легко заметить,
что указанные соотношения весьма напоминают известные ещё из средней школы
обычные алгебраические, если принять, что Æ означает своего
рода ноль, e - единицу, «или»
равнозначно сложению, а сцепление - умножению. Соотношение (2), правда, явно
выбивается из этой логики. Его придётся просто запомнить. Заметим, что одно время «или» также
обозначалось и для множеств знаком «+», но поскольку это противоречит
привычной логике для соотношений 9-11, то позже было решено применять более
точное по отношению ко множествам обозначение «|». Для любого
регулярного выражения существует эквивалентное РВ, которое либо есть Æ, либо не содержит в своей записи Æ. Поэтому в дальнейшем будем
рассматривать только РВ, не содержащие в своей записи Æ. Примеры и задачи на усвоение 3.1. Совпадают
ли множества, соответствующие двум
данным РВ: а) a*b и b +
aa*b; б) b(b+ab)*a и b(b*ab)*b*a; в) b(ab+b)* и bb*a(bb*a)*. Возьмём п. а) и
посмотрим, какие множества соответствуют первому и второму РВ соответственно: a*b = b | ab | aab | …| anb | … b + aa*b = b | ab | aab | …| anb | …, т.е. имеем с
помощью РВ разные записи одного и того же РМ. А вот в задаче в)
ответ отрицательный. Его легко увидеть, если рассмотреть, какие цепочки
наименьшей длины задаются каждым из РВ (с учётом того, что выражение под
итерацией включает пустую цепочку). В первом случае это цепочка b, а во втором – ba. Очевидно, РВ
задают разные РМ. 3.2.
Замените каждое из следующих выражений эквивалентным, в котором не
используются знак "+" (для п. «а» попробуйте найти несколько
решений): а) (a+b)*; б) (a+bb+ba)*. |
|
|||
|
|
3.1. Конечные
автоматы Праволинейные грамматики и регулярные множества и
выражения описывают способ построения всех допустимых цепочек
регулярного языка. Но если мы сможем распознать принадлежность языку любой
произвольной цепочки, то тем самым мы также определим данный язык. Этой цели служат конечные
распознаватели (конечные автоматы, finite automata, общепр. сокр. -
КА). Образно КА можно
представить, например, так: |
|
|||
|
|
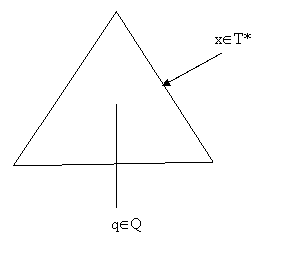
Рис. 3.1. Одно из возможных образных представлений конечного автомата |
|
|||
|
|
Исследуемая
цепочка xÎT* познаково читается КА в соответствии с правилами
переходов из одного допустимого состояния распознавателя (q) в другое (p): d (q, a) = p, q, p Î Q; a – текущий читаемый знак из цепочки x. либо d (q, e) = p, т.е. может быть переход без чтения
входного знака. Условием
допуска (успешного распознавания цепочки на
принадлежность заданному посредством КА языку) является: А. Её полное
прочтение. Б. Попадание КА в
подмножество допускающих состояний F Í Q. Более формально КА – это пятёрка {Q, T, d, q0, F}, где Q – конечное множество (алфавит) состояний
распознавателя; T – алфавит основных знаков (для
разбираемых цепочек); d - множество правил перехода
вышеупомянутого вида; q0 – начальное состояние КА; F – множество допускающих состояний (F Í Q). |
|
|||
|
|
Пример 3.1. КА для языка {x Î {a, b}* : |x|a – чётно}, т.е. все цепочки
из знаков a и b, в которых число
знаков a – чётно. d (S, a) = A d (S, b) = S d (A, a) = S d (A, b) = A (здесь S – допускающее состояние). |
|
|||
|
|
3.2. Диаграмма состояний КА Для большей
наглядности (обозримости) устройства КА распространён способ изображения
автоматов в виде рисунка (упорядоченного графа), также часто называемого
диаграммой состояний, где вершины графа обозначают состояния распознавателя,
а помеченными направленными дугами – переходы из одного состояния в другое. Для нашего
примера диаграмма будет выглядеть так: |
|
|||
|
|
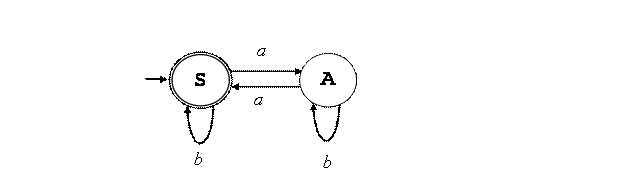
Рис.
3.2. Диаграмма состояний КА для языка {x Î {a, b}* : |x|a - чётно} |
|
|||
|
|
Начальное
состояние помечено входящей стрелкой, допускающие состояния – двойным
контуром. В нашем примере S является и
начальным, и допускающим состоянием. Мысленно
запустим данный распознаватель для цепочки abab: d (S, abab) " d (A, bab) " d (A, ab) " d (S, b) " d (S, e) Цепочка
прочитана полностью, КА находится в допускающем состоянии S, т.е. цепочка принадлежит заданному
языку. |
|
|||
|
|
3.3. Связь КА и ПГ КА
непосредственно могут быть построены по ПГ и обратно. Оба способа имеют
одинаковую выразительную силу. При
переходе КА " ПГ каждое
правило перехода заменяется следующим правилом порождения ПГ: d (q, a) = p на q " ap. Если p Î F, то в правила ПГ дополнительно надо добавить и p " e. А q0
в КА соответствует начальному знаку (аксиоме) ПГ. Пример 3.2. Построим
эквивалентную ПГ для КА по рис. 3.2. Вход. d (S, a) = A;
d (S, b) = S;
d (A, a) = S;
d (A, b) = A. Выход. S " aA | bS | e (для заключит.
состояний добавляется переход в e) A " aS | bA Подобным
образом осуществляется и обратное непосредственное преобразование из ПГ в КА.
Предоставляем опробовать его читателю. В
сети выложено немало описаний по конечным распознавателям и на иностранных
языках, например, [3]. |
|
|||
|
|
3.4. Связь ПГ и РВ РВ
могут быть построены по ПГ путём решения системы уравнений с регулярными
множителями (coefficients). 3.4.1.
Отдельное уравнение с регулярными
коэффициентами x = ax + b (или, в более современном виде записи x = ax | b), где x – неизвестное, а «а» и «b» - регулярные
множители, имеет следующее решение: x = a*b Проверим
это утверждение, подставив предложенное решение в обе части исходного
уравнения: a*b = aa*b | b ? Да,
это так, поскольку a*b соответствует РМ {b, ab, aab, …, anb, …}, а выражение aa*b | b – {ab, aab, …, anb, …} | {b}, т.е. тому
же РМ, только перечисленному в ином
порядке. 3.4.2.
Решение системы уравнений с
регулярными коэффициентами Целью
решения данной системы уравнений (СУ) является получение РВ для аксиомы
исходной ПГ. Это РВ (при правильном решении) и является равнозначным РВ для
исходной ПГ. В
качестве примера возьмём только что рассмотренную нами ПГ: S " aA | bS | e A " aS | bA и
переведём её в РВ. Способ
решения СУ напоминает известный способ Гаусса для решения системы линейных
алгебраических уравнений: последовательно находим решения для отдельных
неизвестных, подставляем их в оставшиеся уравнения и так до тех пор, пока не
найдём решение для аксиомы. В
данном случае для уравнения A = aS | bA или, что тоже самое A = bA | aS (собрали сначала
множители при неизвестном (A), затем
перечислили свободные члены) имеем решение A = b*aS Подставим
его в первое уравнение СУ: S = aA | bS | e S = a b*aS | bS | e После
сборки множителей при неизвестном (S) получим: S = (ab*a | b)S | e и решение этого уравнения S = (ab*a | b)* e = (ab*a | b)* Для
самопроверки можно вернуться к КА, соответствующему исходной ПГ, и посмотреть,
соответствуют ли получаемые РВ цепочки КА хотя бы для простейших случаев.
В
данном случае никаких расхождений с полученным выражением (ab*a | b)* не наблюдается. Этот приём, используя наглядность
представления КА, нередко позволяет вовремя выявить допущенные неточности при
решении СУ с регулярными коэффициентами. Дополнительные
сведения по решению уравнений с регулярными коэффициентами приведены,
например, в [4]. Задачи
для самостоятельного изучения 3.3. Найдите РВ,
обозначающие языки, все слова которых --- элементы множества {0,1}*. а) оканчивающиеся
на 011, 101, 110; б) не содержащие
ни одной из подстрок 011 и 101; 3.4.
Для языка {x Î {a, b}* : |x|a – чётно, |x|b - чётно} постройте
по изученным алгоритмам КА, по нему ПГ, а по ней – РВ. Замечание. Если вы точно следуете известным и доказанным алгоритмам, то и
полученное решение считается доказанным. При любых отступлениях от доказанных
подходов (innovation, optimization, etc.) правильность полученного решения придётся доказывать отдельно (по
крайней мере, на контрольных и экзаменах). |
|
|||
|
|
== Ссылки == [1] Серебряков
В.А. [и др.] Теория и
реализация языков программирования. М.: МЗ-Пресс, 2003 (1-е изд.) и 2006 (2-е
изд). – 294 c. (681.3/ Т33). [2] Курочкин В.М.,
Столяров Л.Н., Сушков Б.Г., Флёров Ю.А. Теория и
реализация языков программирования:
Курс лекций. М.: МФТИ, 1978. [3]. Finite automata. Short conspectus. [4]. Дополнительные сведения по решению
уравнений с регулярными коэффициентами (конспект, 4 стр.) (в виде .dvi,
22 Кб, в виде .ps, 109 Кб, в виде .pdf,
143 Кб). |
|
|||
|
|
|
||||
|
|
|
|
|||